动态规划2：最长公共子序列问题

引言

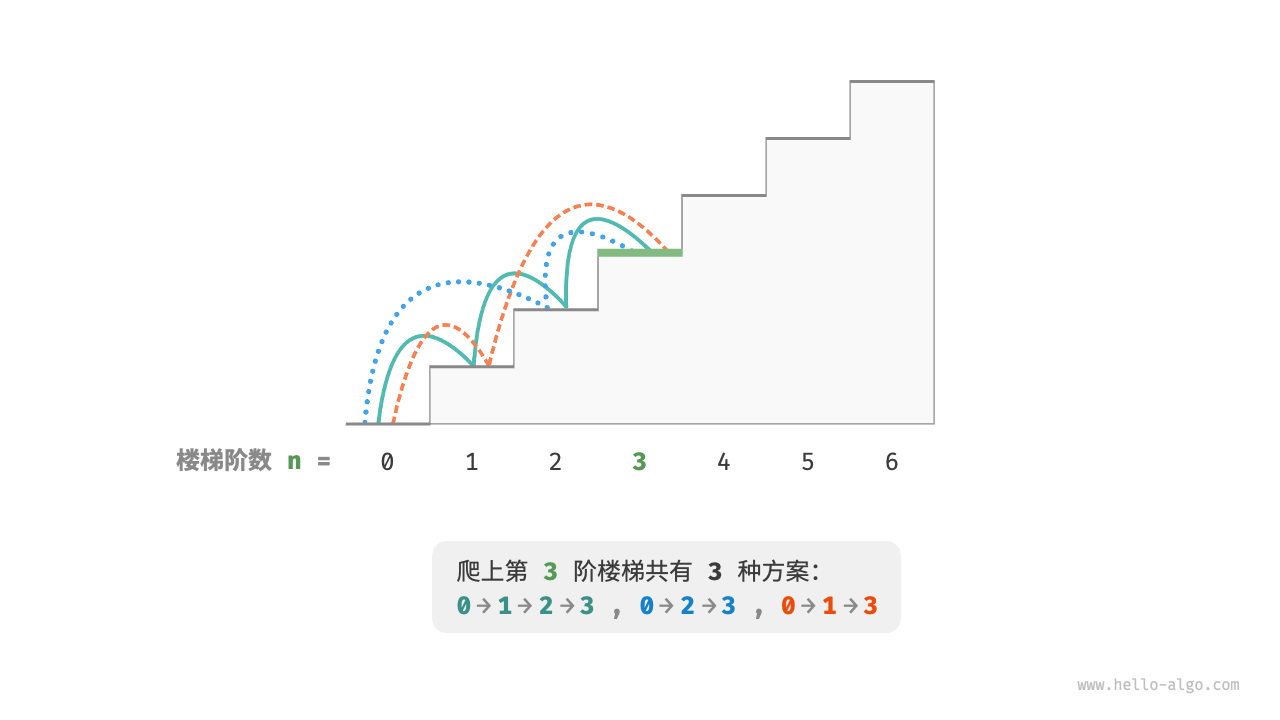
在上一篇文章中，我们通过爬楼梯问题初步了解了动态规划的基本思想。今天，我们将深入学习一个更加经典且实用的动态规划问题——最长公共子序列（Longest Common Subsequence，LCS）。

这个问题不仅在算法面试中频繁出现，在实际开发中也有广泛应用，比如：

版本控制系统中的文件差异比较
生物信息学中的DNA序列比对
文本编辑器的智能提示功能

问题定义

什么是子序列？

首先，我们需要明确子序列的概念：

子序列：从原序列中按照相对顺序选取若干元素组成的新序列
注意：子序列不要求连续，但必须保持相对顺序

例如，对于字符串 "ABCDEF"：

"ACE" 是一个子序列 ✅
"BDF" 是一个子序列 ✅
"CAB" 不是子序列 ❌（顺序错误）

最长公共子序列问题

给定两个序列，找到它们的最长公共子序列的长度。

例题：LeetCode 1143. 最长公共子序列

1
2
3

输入：text1 = "abcde", text2 = "ace" 
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。

解题思路

1. 暴力解法思考

最直观的想法是枚举第一个字符串的所有子序列，然后检查每个子序列是否也是第二个字符串的子序列。但这种方法时间复杂度为 O(2^n × m)，对于长字符串来说效率太低。

2. 动态规划思路

让我们从状态定义开始思考：

状态定义：

dp[i][j] 表示 text1[0...i-1] 和 text2[0...j-1] 的最长公共子序列长度

状态转移：
当我们考虑 text1[i-1] 和 text2[j-1] 时：

如果字符相等：text1[i-1] == text2[j-1]
1
dp[i][j] = dp[i-1][j-1] + 1
如果字符不相等：text1[i-1] != text2[j-1]
1
dp[i][j] = max(dp[i-1][j], dp[i][j-1])

边界条件：

dp[0][j] = 0（空字符串与任何字符串的LCS长度为0）
dp[i][0] = 0（同上）

图解分析

让我们通过一个具体例子来理解这个过程：

text1 = "ace", text2 = "aec"

创建二维DP表格：

    ""  a   e   c
""   0   0   0   0
a    0   1   1   1
c    0   1   1   2
e    0   1   2   2

填表过程：

初始化边界：第一行和第一列都是0
填充 dp[1][1]：比较 ‘a’ 和 ‘a’
- 相等：dp[1][1] = dp[0][0] + 1 = 1
填充 dp[1][2]：比较 ‘a’ 和 ‘e’
- 不相等：dp[1][2] = max(dp[0][2], dp[1][1]) = max(0, 1) = 1
继续填充…

最终答案：dp[3][3] = 2，表示LCS长度为2。

代码实现

Java实现

public class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length();
        int n = text2.length();
        
        // 创建DP表格，大小为(m+1) x (n+1)
        int[][] dp = new int[m + 1][n + 1];
        
        // 填充DP表格
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    // 字符相等，LCS长度+1
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    // 字符不相等，取较大的LCS长度
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        
        return dp[m][n];
    }
}

Python实现

def longestCommonSubsequence(text1: str, text2: str) -> int:
    m, n = len(text1), len(text2)
    
    # 创建DP表格
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    
    # 填充DP表格
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if text1[i - 1] == text2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
    
    return dp[m][n]

空间优化

由于每次计算只需要前一行的信息，我们可以将空间复杂度从 O(m×n) 优化到 O(min(m,n))：

public int longestCommonSubsequence(String text1, String text2) {
    // 确保text1是较短的字符串
    if (text1.length() > text2.length()) {
        return longestCommonSubsequence(text2, text1);
    }
    
    int m = text1.length();
    int n = text2.length();
    
    // 只需要两行
    int[] prev = new int[m + 1];
    int[] curr = new int[m + 1];
    
    for (int j = 1; j <= n; j++) {
        for (int i = 1; i <= m; i++) {
            if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                curr[i] = prev[i - 1] + 1;
            } else {
                curr[i] = Math.max(prev[i], curr[i - 1]);
            }
        }
        // 交换prev和curr
        int[] temp = prev;
        prev = curr;
        curr = temp;
    }
    
    return prev[m];
}

复杂度分析

时间复杂度：O(m × n)，其中 m 和 n 分别是两个字符串的长度
空间复杂度：
- 未优化版本：O(m × n)
- 优化版本：O(min(m, n))

扩展问题

1. 输出具体的LCS

如果需要输出具体的最长公共子序列，我们可以通过回溯DP表格来实现：

public String getLCS(String text1, String text2) {
    int m = text1.length();
    int n = text2.length();
    int[][] dp = new int[m + 1][n + 1];
    
    // 填充DP表格（同前面的代码）
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    
    // 回溯构造LCS
    StringBuilder lcs = new StringBuilder();
    int i = m, j = n;
    
    while (i > 0 && j > 0) {
        if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
            lcs.append(text1.charAt(i - 1));
            i--;
            j--;
        } else if (dp[i - 1][j] > dp[i][j - 1]) {
            i--;
        } else {
            j--;
        }
    }
    
    return lcs.reverse().toString();
}