动态规划1:从爬楼梯问题开始
前言
动态规划(Dynamic Programming,简称DP)是算法设计中的一种重要思想,它通过将复杂问题分解为子问题,并存储子问题的解来避免重复计算,从而提高算法效率。
作为动态规划系列的第一篇文章,我们将从最经典的入门题目——LeetCode第70题”爬楼梯”开始,深入理解动态规划的核心思想。
什么是动态规划?
动态规划的核心思想是:将一个问题分解为若干个子问题,通过求解子问题并保存其结果,避免重复计算,最终得到原问题的解。
动态规划通常具备以下特征:
- 最优子结构:问题的最优解可以通过子问题的最优解来构造
- 重叠子问题:在求解过程中,同一个子问题会被多次计算
- 无后效性:一旦确定某阶段的状态,则此后过程的演变不再受此前各种状态及决策的影响
LeetCode 70. 爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
1 | 输入:n = 2 |
示例 2:
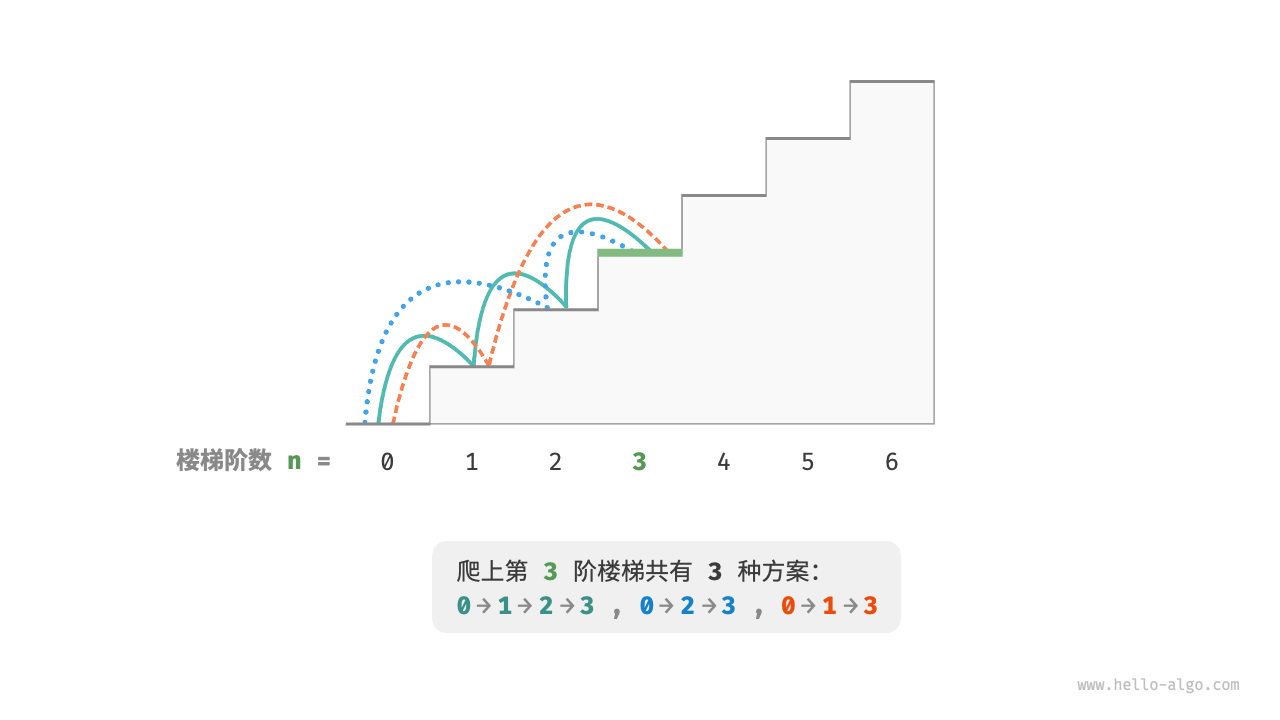
1 | 输入:n = 3 |
思路分析
这是一个典型的动态规划问题。让我们一步步分析:
1. 寻找状态转移方程
要到达第 n 阶台阶,我们只能从第 n-1 阶或第 n-2 阶到达:
- 从第
n-1阶走 1 步 - 从第
n-2阶走 2 步
因此,到达第 n 阶的方法数 = 到达第 n-1 阶的方法数 + 到达第 n-2 阶的方法数
状态转移方程:f(n) = f(n-1) + f(n-2)
2. 确定初始状态
f(1) = 1:到达第1阶只有1种方法f(2) = 2:到达第2阶有2种方法(1+1 或 2)
3. 递推求解
通过状态转移方程,我们可以从初始状态开始,逐步计算到 f(n)。
解法实现
方法一:递归(会超时)
1 | def climbStairs(n): |
时间复杂度: O(2^n) - 存在大量重复计算
空间复杂度: O(n) - 递归栈深度
方法二:动态规划(一维数组)
1 | def climbStairs(n): |
时间复杂度: O(n)
空间复杂度: O(n)
方法三:空间优化的动态规划
1 | def climbStairs(n): |
时间复杂度: O(n)
空间复杂度: O(1)
Java版本实现
1 | public class Solution { |
执行过程演示
让我们以 n = 5 为例,演示动态规划的计算过程:
1 | f(1) = 1 |
所以爬到第5阶有8种不同的方法。
动态规划的解题步骤
通过这个例子,我们可以总结出动态规划的一般解题步骤:
- 定义状态:确定用什么来表示一个子问题
- 找状态转移方程:子问题之间的递推关系
- 确定初始状态和边界情况:递推的起点
- 确定计算顺序:保证计算某个状态时,依赖的状态已经计算出来
- 空间优化(可选):如果只依赖前几个状态,可以用滚动数组优化空间
举一反三
爬楼梯问题实际上就是斐波那契数列的变形。类似的问题还有:
- LeetCode 198. 打家劫舍:每间房屋都有一定金额,不能连续偷相邻房屋
- LeetCode 746. 使用最小花费爬楼梯:每一阶都有花费,求最小花费到达顶部
- LeetCode 509. 斐波那契数:直接求斐波那契数列第n项
总结
爬楼梯问题是动态规划的经典入门题目,它帮助我们理解了:
- 如何识别动态规划问题的特征
- 如何找到状态转移方程
- 如何进行空间优化
- 动态规划相比递归的优势
在下一篇文章中,我们将继续探讨更复杂的动态规划问题,包括二维DP、背包问题等。敬请期待!
相关链接:
标签: #动态规划 #算法 #LeetCode #面试必备
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 DevGobang!